Increasingly traffic analysis makes use of complex statistical techniques, which are not (yet) part of the standard training of computer scientists at Cambridge (UK). As aresult I spend a lot of time reading textbooks like the excellent Bayesian Data Analysis(by Andrew Gelmanet al, who also maintains a blog) or Information Theory, Inference, and Learning Algorithms by David MacKay, who treats the subject more from a Computer Science perspective. The most fascinating aspect Bayesian statistics is that it is very easy (and even intrinsic to the analysis) to calculate one’s confidence in an inferred assertion.
One question that has been in my mind for some time is whether any Cambridge Colleges are better or worse on average than any others in Computer Science. Being `better’ is a very subjective judgement when it comes to education, but the primary issue that I wanted to study is whether one could claim that students of any particular college get consistently better or worse exam marks than others. Luckily the class marks for Part IB and Part II computer science were recently published (on a physical notice board — sorry no link) for the 2008 exams which could be subject to analysis to answer that question. But what would be the right way of doing this?
A simple minded approach would involve taking the proportion of students that got high marks (a First or Two-one) and rank colleges accordingly. Any college that is in the bottom half of this ranking is underperforming, while any college in the top half is doing well. Yet this approach gives no intuition about how significant the resutls are: different colleges have different number of students, and these numbers are in any case very small. It is likely that the resulting ranking is subject to random fluctiations.
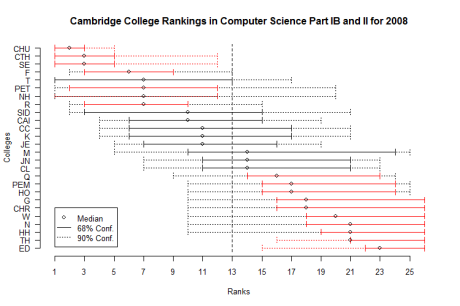
Instead I construct a simple Bayesian model for the ranking of colleges, which readily leads itself to calculating the confidence an observer can have about the assigned ranks. The resulting graph plots the rank of each college, along with the 68% (solid line) and 90% (dotted line) confidence interval over that rank. Red intervals indicate that the college is significantly over or below average.
Only a handful of colleges turn out to be significanlty (i.e. more than 90% of the time) better or worse in terms of exam resutls. For the record, Churchill, St Catherine’s, Selwyn, and Fitzwilliam are definitely above average. For all others the small number of students in a single year makes it impossible to tell if the colleges are systematically or randomly getting high or low marks. There is an interesting correlation between these results and physical proximity to the Computer Laboratory!
A few more details on the model used to derive the above graph: The model assumes that each college i has a (hidden) variable pi in [0,1] representing the probability that a student at this college receives a First or Two-one (observed) mark (each student independently receives such a mark with probability pi and a binomial distribution describes the number of marks above average that each college receives, according to their number of students.) Colleges are ranked according to their respective probabilities pi, from highest to lowest.
The problem is then transformed into a simple Bayesian inference exercise: given the observed marks we need to estimate the hidden pi, for each college. We model our belief about each pi as a Beta distribution, with a non-informative prior Beta(a=1,b=1). We update the distribution according to the observations, and it becomes for each college pi ~ Beta(a=1+#(High Marks), b=1+#(Low Marks)). We then draw samples from those distributions and rank the colleges. We repeat this procedure about 55,000 times (that should be large enough) and calculate the intervals in which the college ranks lie 68% and 90% of the time. A Python script generates the samples and an R script produces the plot.
Disclaimer: there is no causation implied between college and marks. This correlation could be due to colleges selecting students in particular ways, teaching them better, or ensuring that they leave university instead of getting low marks. There is no way of telling which apply from this analysis. It is totally wrong to judge colleges just based on such exam performance statistics, and as the results show, most of the time statistically meaningless.